Acesse o conteúdo completo – Resumo dos algoritmos de ordenação para o CNU (TI)
Olá estudante, tudo bem? Neste artigo apresentaremos um resumo dos principais algoritmos de ordenação para o concurso do CNU: algoritmo da bolha, algoritmo de ordenação por seleção e algoritmo de ordenação por inserção.
Questões de algoritmos de ordenação são muito comuns em provas da Cesgranrio, sendo que a probabilidade de que caia alguma questão na prova do CNU é muito grande.
A ideia deste artigo é apresentar um resumo rápido desses algoritmos de ordenação, abordando os seguintes tópicos:
- Algoritmo de Ordenação da Bolha
- Algoritmo de Ordenação por Seleção
- Algoritmo de Ordenação por Inserção
- Desempenho dos Algoritmos de Ordenação
- Quadro comparativo dos algoritmos de ordenação
- Questões para praticar
Algoritmo de Ordenação da Bolha (Bubble Sort)
O método da bolha consiste em percorrer uma lista, comparando elementos que estão lado a lado (pares consecutivos) e trocando suas posições se estiverem fora de ordem. Em cada passo, o maior elemento “flutua” para a última posição, e este processo é repetido até que todos os elementos estejam na ordem correta.
Aqui está um exemplo de como ordenar a lista [8, 2, 3, 5, 1]:
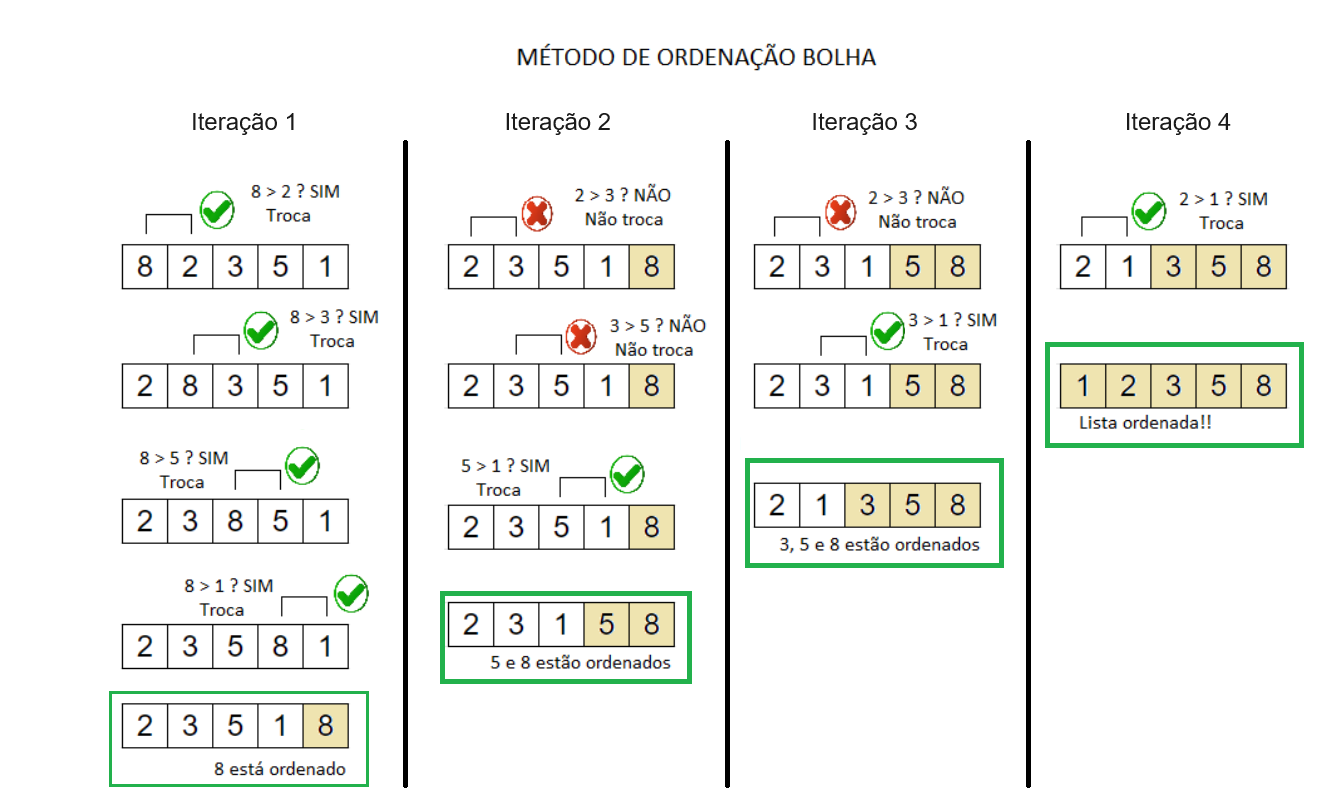
Perceba que a cada iteração, o maior elemento entre aqueles que ainda não foram ordenados é movido para a última posição. É importante notar que durante esse processo, ocorreram 10 comparações e 7 trocas.
No método da bolha, o número de comparações realizadas pode ser calculado usando a seguinte fórmula: comparações = N * (N – 1) / 2, onde N representa o número de elementos presentes na lista.
Algoritmo de Ordenação por Seleção (Selection Sort)
O algoritmo de ordenação por seleção opera escolhendo o menor elemento de uma lista desordenada e colocando-o na primeira posição. Isso é repetido em cada iteração, removendo os elementos já ordenados. Em outras palavras, a cada passo, seleciona-se o menor elemento da parte não ordenada da lista e o posiciona no início.
Aqui está uma representação visual de um exemplo de ordenação utilizando o algoritmo de seleção com a lista [6, 2, 3, 5, 1, 4]:
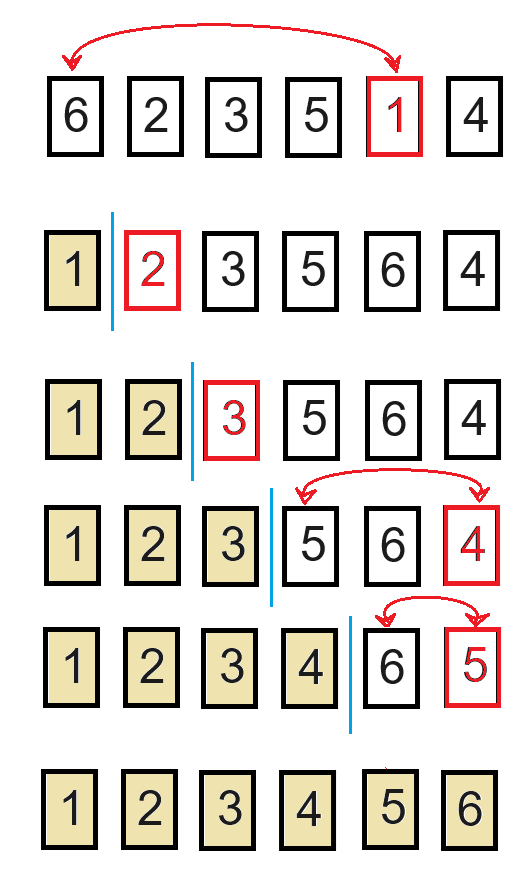
Observe que a cada iteração o menor elemento dentre os não ordenados é trocado pelo primeiro elemento deles. O algoritmo realiza, no máximo, uma troca a cada iteração. Uma desvantagem deste algoritmo é que mesmo com lista já ordenada, ele compara todos os elementos da parte não ordenada por ele para descobrir o menor elemento.
Por exemplo, perceba que depois da primeira iteração, os elementos 2 e 3 já estão ordenados. Mesmo assim, o algoritmo faz as comparações com os demais elementos para “ter certeza” de que realmente eles são os menores elementos.
Nesse exemplo, o algoritmo ao todo faz 15 comparações e apenas 3 trocas, pois na segunda e terceira iteração não são realizadas trocas.
As comparações são realizadas para encontrar o menor elemento. Na primeira iteração, o algoritmo compara os seis elementos, ou seja, realiza 5 comparações. Na segunda iteração, como o primeiro elemento já está ordenado, o algoritmo só compara os cinco elementos restantes, realizando quatro comparações.
Assim como no método da bolha, a fórmula C = n * (n-1) / 2 encontra o número de comparações realizadas pela ordenação por seleção.
Algoritmo de Ordenação por Inserção (Insertion Sort)
O algoritmo de ordenação por inserção funciona assim: você divide a lista em duas partes, uma parte ordenada e outra desordenada. Em cada passo, pega-se o primeiro elemento da parte desordenada e o coloca na posição correta da parte ordenada. Repete-se esse processo até que todos os elementos estejam na parte ordenada e a lista esteja completamente ordenada.
Aqui está uma representação visual de um exemplo de ordenação utilizando o algoritmo de inserção com a lista [6, 2, 3, 5, 1, 4]:
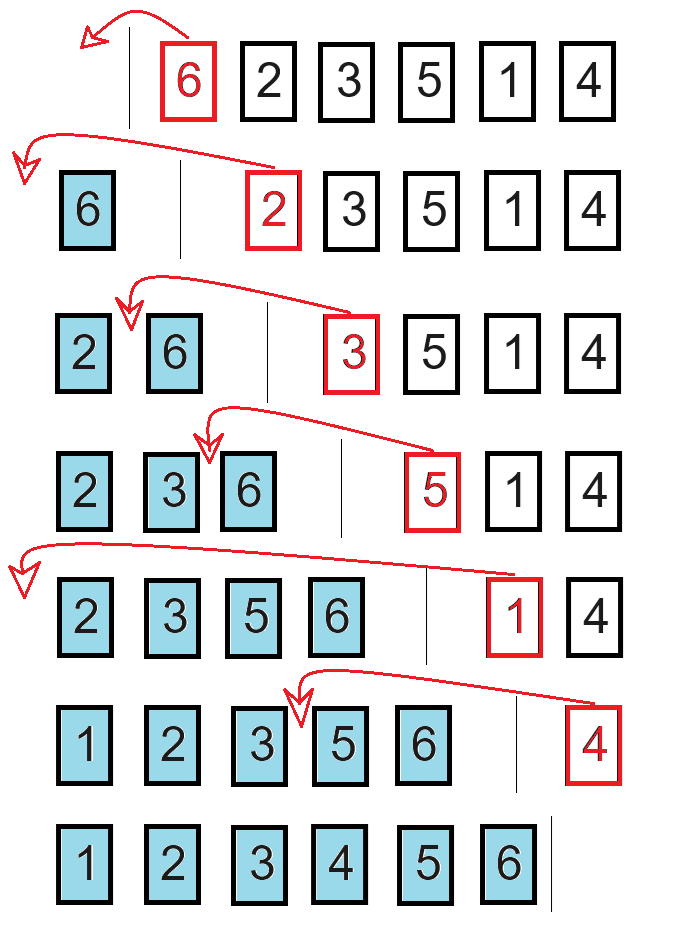
Observe que no início, o elemento 6 é considerado como ordenado. Em seguida, o algoritmo seleciona o primeiro elemento não ordenado e o insere na posição correta entre os elementos ordenados. Por exemplo, se tivermos a parte ordenada [2, 6] e o elemento 3 for selecionado, ele será inserido entre os dois valores, resultando em [2, 3, 6]. No final, a lista estará totalmente ordenada.
Em resumo, o número de comparações e movimentações feitas pelo algoritmo varia dependendo do grau de ordenação da lista. Para listas com pouca ordenação, muitas comparações e movimentações são necessárias. Por outro lado, para listas quase ordenadas, apenas algumas comparações e movimentações são necessárias.
Desempenho dos Algoritmos de Ordenação
Complexidade dos algoritmos de ordenação
Aqui está um quadro comparativo da complexidade dos algoritmos de ordenação bolha, por seleção e por inserção nos casos pior, médio e melhor:
| Algoritmo de Ordenação | Pior Caso | Caso Médio | Melhor Caso |
| Bolha | O(n^2) | O(n^2) | O(n^2)** |
| Seleção | O(n^2) | O(n^2) | O(n^2) |
| Inserção | O(n^2) | O(n^2) | O(n) |
** Uma variação do método bolha com condição de parada tem complexidade linear, ou seja, N, no melhor caso, isto é, quando a lista está ordenada. Neste caso, o algoritmo apenas percorre a lista uma vez, e estando ela ordenada, finaliza a execução.
O algoritmo de ordenação por inserção possui no melhor caso a complexidade de N.
Por fim, o pior e o médio caso para todos os três algoritmos são O(n^2), o que significa que eles são menos eficientes em conjuntos de dados não ordenados ou grandes.
Em resumo, temos:
- Pior e médio caso: os três algoritmos tem complexidade quadrática (n²)
- Melhor caso:
- Ordenação por seleção: complexidade quadrática, ou seja, n².
- Ordenação por inserção: complexidade linear, ou seja, n.
- Método da bolha:
- algoritmo tradicional da bolha: complexidade quadrática,
- algoritmo com condição de parada: complexidade linear.
Eficiência dos algoritmos de ordenação
Entre os três algoritmos de ordenação discutidos neste resumo, o menos eficiente é o algoritmo da bolha. Embora seja fácil de entender, na prática ele é mais lento em comparação com os outros algoritmos de mesma complexidade, devido ao grande número de movimentações e comparações que requer.
Por outro lado, o algoritmo de ordenação por seleção tem menos movimentações, tornando-o vantajoso para ordenar estruturas complexas. No entanto, uma desvantagem é que o número de comparações é o mesmo para todas as listas, inclusive as que já estão ordenadas.
Por último, o algoritmo de ordenação por inserção demonstra o melhor desempenho na prática em comparação com os outros dois. O número de comparações e movimentações depende do nível de ordenação da lista. Em uma lista totalmente reversa, o número de comparações e movimentações é alto, mas em uma lista já ordenada, é mínimo, resultando em uma complexidade linear nesse caso. Enfim, este algoritmo é recomendado para conjuntos pequenos de dados.
Quadro comparativo dos principais algoritmos de ordenação
O quadro abaixo apresenta um resumo comparativo dos algoritmos de ordenação bolha, por seleção e por inserção:
| Característica | Bolha | Seleção | Inserção |
| Complexidade | O(n^2)O(n^2)O(n) | O(n^2)O(n^2)O(n^2) | O(n^2)O(n^2)O(n) |
| Eficiência | Baixa | Média | Alta para pequenos conjuntos de dados |
| Estabilidade | Estável | Não estável | Estável |
| Modo de operação | Comparações consecutivas | Seleção do menor elemento | Inserção ordenada |
| Uso | Pouco comum | Pouco comum | Comum em listas encadeadas ou pequenos conjuntos de dados |
- Complexidade: Refere-se ao número de operações que o algoritmo realiza para ordenar um conjunto de dados.
- Eficiência: Refere-se à velocidade do algoritmo em ordenar um conjunto de dados.
- Estabilidade: Refere-se à capacidade de manter a ordem relativa dos elementos iguais em um conjunto de dados durante a ordenação.
- Modo de operação: Refere-se à maneira como o algoritmo funciona para ordenar um conjunto de dados.
Questão 1
Ano: 2014 Banca: CESGRANRIO Órgão: Petrobras Prova: CESGRANRIO – 2014 – Petrobras – Técnico(a) de Informática Júnior
Os algoritmos de ordenação por seleção (SS) e bubble sort (BS) foram usados para ordenar a sequência 31, 11, 23, 17, 13 de forma crescente.
Quantas trocas e comparações foram realizadas, respectivamente, por cada um?
a) SS – 3 e 10 / BS – 7 e 10
b) SS – 3 e 11 / BS – 8 e 16
c) SS- 8 e 16/ BS – 3 e 11
d) SS – 7 e 16 / BS – 3 e 10
e) SS- 4 e 11/ BS – 8 e 16
Comentário:
Pela fórmula do número de comparações do algoritmo de ordenação por seleção e bolha já mataríamos a questão. Veja que a lista possui 5 elementos, logo:
C = n * (n – 1) / 2;
C = 5 * 4 / 2;
C = 10.
Assim, tanto o método da bolha, quanto a ordenação por seleção fazem 10 comparações. Dessa forma, a única alternativa que possui 10 comparações para o algoritmo de ordenação por seleção e da bolha é a letra A.
Mas, para o desencargo de consciência, vamos verificar o número de trocas realizadas.
Vejamos:
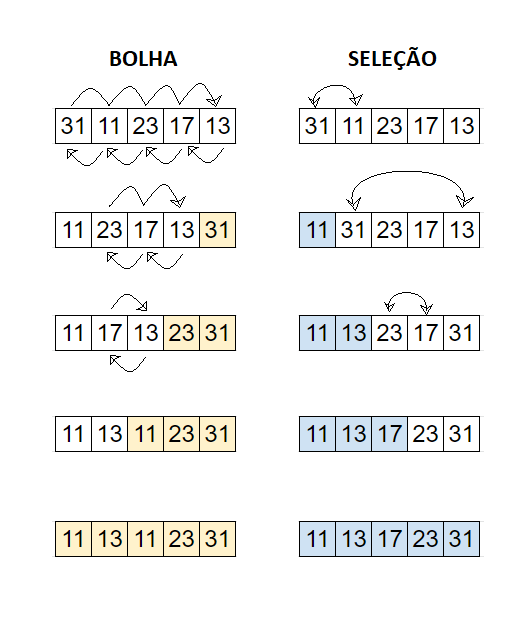
Observe que no método bolha tivemos 7 trocas e na ordenação por seleção tivemos 3 trocas.
Portanto, a letra A é a alternativa correta.
Questão 2
Ano: 2011 Banca: CESGRANRIO Órgão: FINEP Prova: CESGRANRIO – 2011 – FINEP – Analista – Desenvolvimento de Sistemas
Considerando-se a análise assintótica (Notação Big O), qual é a complexidade do caso médio do algoritmo de ordenação chamado de Ordenação por Inserção?
a) O(n²)
b) O(1)
c) O(n)
d) O(n log n)
e) O(log n)
Comentários:
A complexidade do algoritmo de ordenação por inserção é:
- Pior caso e caso médio: n²
- Melhor caso: n
Portanto, a letra A é a alternativa correta.
Questão 3
Ano: 2021 Banca: CESGRANRIO Órgão: Banco do Brasil Prova: CESGRANRIO – 2021 – Banco do Brasil – Agente de Tecnologia
Dentre os problemas identificados pela gerência de um banco comercial, está a localização das contas dos seus titulares nas listagens e nos relatórios impressos em diferentes situações. Um especialista de TI sugeriu ordenar as contas por meio dos CPF dos seus n titulares antes das impressões.
Dentre alguns algoritmos pré-selecionados para essa ordenação, o especialista escolheu o algoritmo de ordenação por inserção, no qual o consumo de tempo é, no melhor caso, proporcional a
a) n log n
b) log n
c) n²
d) n
e) 1
Comentários:
Questão bem semelhante à anterior. A complexidade do algoritmo de ordenação por inserção é:
- Pior caso e caso médio: n²
- Melhor caso: n
Portanto, a letra D é a alternativa correta.
Conclusão
Bom pessoal, terminamos por aqui este artigo. Procuramos apresentar um resumo dos pontos mais importantes dos principais algoritmos de ordenação para concursos públicos. Espero que o conteúdo aqui apresentado seja útil em sua jornada rumo à aprovação.
Quer saber quais serão os próximos concursos?
Confira nossos artigos!
Concursos abertos
Concursos 2024
Fonte: Estratégia Concursos

