Fique por dentro – Logaritmos para a SEFAZ-AC

Fala, pessoal! Tudo certo? Faltando poucos dias para a realização da prova do Concurso da Secretaria da Fazenda do Estado do Acre (SEFAZ-AC), trouxe um assunto que julgo importante: Logaritmos.
Contudo, você que está se preparando para esse concurso deve estar se perguntando: “Ué, mas não há previsão de logaritmos para a SEFAZ-AC nos assuntos de Matemática Financeira e Raciocínio Lógico”.
Pois é, ilibado concurseiro, diretamente não há previsão, mas PODE aparecer em questões principalmente de matemática financeira. Por isso nossa aposta!!

Origem dos logaritmos e para que serve

Vamos iniciar com uma breve citação:

O termo logaritmo foi criado pelo escocês John Napier: de logos e arithmos, que significam, respectivamente, “razão” e “número”. E a obra em que, no ano de 1614, apresentou essa sua descoberta recebeu o título de Miriface Logarithmorum canonis descriptio(ou seja, uma descrição da maravilhosa regra dos logaritmos).
(Fonte: Fundamentos de matemática elementar – Editora Atual. Iezzi et al, p. 55).

Ademais, trazendo para a nossa realidade, o logaritmo veio para que possamos resolver expressões que possuem bases diferentes. Se nos depararmos com a seguinte expressão: 2^x = 3^x , como fazer?
E aí que entram os logaritmos e suas propriedades. Neste artigo vamos demonstrar as mais importantes.

Definição dos logaritmos

De início, saibamos que:

log_ab = x. Que por definição: a^x = b.

Só com essa definição já conseguimos resolver diversas questões. Traduzindo em texto, temos: “Sendo que a e b são números reais e positivos, com a diferente de 1 (a≠1), chama-se logaritmo de b na base a. E x é o expoente que se deve dar à base a de modo que a potência obtida seja igual a b.

Consequências da definição.

Pessoal, da definição acima temos algumas consequências que preciso que memorizem.

• LOG_a1 = 0, pois transformando em exponenciação teríamos: a⁰ = 1. E todo número elevado a 0(zero) é um.
• Transformando em exponenciação, conseguimos chegar à outra propriedade: LOG_aa  = 1;
• A^LOG_a^B  = B; Aqui, a base A com a base do logaritmo(a) se anulam, restando, portanto, apenas B
• Log_aB = Log_aC é B=C, pois as bases de anulam.

Propriedades básicas importantes

Vamos agora às principais propriedades/transformações de logaritmos para a SEFAZ-AC que serão muito úteis em questões de matemática financeira. Seguem:

No que se refere à ultima transformação acima, o quociente do logaritmo pode ser qualquer outra raiz, não necessariamente raiz quadrada. Usamo-la por ser a mais comum, ok??!
Com essas transformações, vocês conseguem “matar” quase todas as questões que cobram esse conteúdo.

Mudança de base

Já essa propriedade é um pouco mais “chatinha”, mas vamos juntos. Por vezes as questões darão dados logarítmicos em bases diferentes. Assim pois, precisaremos alterar a base para usá-los. Contudo, como alterar?
Se a, b, c são números reais positivos e a e c diferentes de 1(as bases sempre são diferentes de 1), chegaremos nessa propriedade. Vamos alterar a base de “a” para “c”:

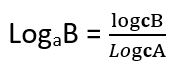
Desta feita, vamos supor que para determinada questão você precise saber o valor de Log₂32, mas a questão só lhe forneceu que Log₄8 = 1,5, como fazer?

Para isso, você pode passar o Log de base 2 para a base 4. Ficaria assim: Log₂32 = (Log₄32 / Log₄2). Vamos aplicar as demais regras estudadas. Primeiramente, 32 = (8 x 4) e 2 = 4^1/2.Com isso, teríamos: (Log₄8 + Log₄4)/ (1/2 x Log₄4). Logo, tinha-se: (1,5 + 1)/0,5. Então, Log₂32 = 5.

Aplicando os conhecimentos das propriedades estudadas

Questão 1

Vamos iniciar com uma questão da CESGRANRIO – 2023 (Escriturário BANRISUL)
Um investidor planeja ter um montante superior a 600 mil reais e, para isso, aplicou uma única quantia de 200 mil reais, em janeiro de 2023, a uma taxa fixa de 12% ao ano, no regime de juros compostos, conforme orientação do consultor financeiro indicado pelo gerente do banco. Supondo-se que ele não faça mais nenhum aporte no investimento, o número mínimo de anos, para ser atingida a meta, por meio, exclusivamente, desse investimento, é igual a

Dado:
log 1,12 = 0,049;
log 3 = 0,477
Comentários: Percebemos que se trata de uma questão simples de juros compostos, não fosse pelos logaritmos.
A formula dos juros compostos é: : M=C(1+i)ⁿ, Certo?
O aplicador quer ter, no mínimo, R$ 600.000 ao final do período de aplicação que não conhecemos, sendo o valor inicial R$ 200.000.
Substituindo, temos:
600.000<200.000(1 + 0,12)ⁿ
Para fins de cálculo, vamos igualar a expressão(tirar o sinal de maior que):
600.000 = 200.00(1 + 0,12)ⁿ
Passando o 200.000 dividindo, temos:
600.000/200.000 = 1,12ⁿ
Logo, 1,12ⁿ = 3.
Aqui, precisamos usar os dados fornecidos.
Vamos inserir log decimal dos dois lados. Obs. Pessoal, o log base 10 ou log10 é o mais usado e conhecido. Quando a questão trouxe somente “log” sem a base, estamos falando da base decimal, ok?
Pois bem, Log 1,12ⁿ = Log 3
Aplicando a propriedade do expoente, temos:
n. Log 1,12 = Log 3
n. 0,049 > 0,477
n > 9,73.
Gabarito: Mínimo 10 anos.

Questão 2

Vamos a mais uma questão, porém com um nível de dificuldade maior.
FCC – 2015 – Analista do Tesouro Estadual (SEFAZ PI)
Um capital de R$ 15.000,00 é aplicado, durante 2 anos, à taxa de 5% ao semestre com capitalização contínua. Dos valores abaixo, o mais próximo do valor dos juros desta aplicação é
Dados:
ln(1,051271) = 0,05; ln(1,105171) = 0,10; ln(1,161834) = 0,15 e
ln(1,221403) = 0,20; em que ln é o logaritmo neperiano, tal que
ln(e) = 1.
Comentários: Imaginem uma questão dessas na hora da prova?
Bem, esse ln significa que o logaritmo é neperiano. Também pode ser representando por Log_eX, em que “e” é o número de Euler, que vale aproximadamente 2,71. Além do que, as propriedades são similares ao logaritmo mais comum que estudamos.
Para essa questão, também precisamos saber a fórmula da capitalização contínua:
M = C.e^i.n , em que i é a taxa e n é o período.
Aplicando a fórmula acima, temos:
M = 15.000 X e^{0,05 x 4}
No caso aqui, nobres, temos que lembrar de colocar o tempo coincidindo com a capitalização. Logo, 2 anos são 4 semestres.
Por consequência, M = 15.000 X e^0,2
Vamos aplicar a propriedade da exponenciação com os dados fornecidos:
ln(1,221403) = 0,20; então, e^0,2 = 1,221403. Opa!!
Assim sendo, M = 15.000 X 1,221403.
M = 18.321,00(aproximadamente).
Com efeito, os juros são: J = 18.321,00 – 15.000,00. Nesse sentido, gabarito: J = R$ 3.321,00.

Conclusão

Desta forma, finalizamos aqui, caros concurseiros, o tema logaritmos para a SEFAZ-AC. Esperamos que gostem. Lembrem-se de que para melhor assimilação, é necessário fazer muitas questões. Para isso, usem nosso sistema de questões disponível no link abaixo:
https://www.estrategiaconcursos.com.br/assinaturas/
Bons estudos!

Quer mais informações acerca do concurso da SEFAZ-AC?

cebraspe.org.br/concursos/sefaz_ac_23

Quer estar antenado aos próximos concursos previstos? Confira nossos artigos!

Concursos abertos

Concursos 2024

Material para a SEFAZ AC