Acesse o conteúdo completo – Equivalências Lógicas
Aprenda os conceitos essenciais sobre equivalências lógicas com um resumo para as principais provas de concursos.
Olá, pessoal! Tudo bem com vocês?
As equivalências lógicas são um dos temas mais recorrentes em provas de Matemática e Raciocínio Lógico. Compreender essas relações é essencial para resolver questões de bancas como FGV, CEBRASPE e FCC, que envolvem negações, condicionais, disjunções e bicondicionais — especialmente quando a banca pede para identificar sentenças logicamente equivalentes.
Neste artigo, vamos explorar diversos tipos de equivalências, com explicações e exemplos que facilitam a compreensão, para que você possa revisar a matéria de forma rápida e estratégica.
Confira os tópicos que serão abordados:
- O que são equivalências lógicas? ;
- Equivalências fundamentais;
- Equivalências da condicional;
- Equivalências da bicondicional;
- Outras equivalências lógicas;
O Que São Equivalências Lógicas?
Duas proposições são equivalentes logicamente quando apresentam os mesmos valores de verdade em todas as possíveis combinações de suas variáveis. Ou seja, duas expressões são equivalentes se suas tabelas-verdade forem idênticas.
Em outras palavras, independentemente de os componentes serem verdadeiros ou falsos, as duas expressões assumem o mesmo resultado lógico.
Por exemplo:
- “Se chove, então o chão molha.”
- “Se o chão não molha, então não chove.”
Essas duas proposições são equivalentes, pois expressam a mesma relação de causa e efeito sob forma lógica diferente. Por outro lado, as proposições abaixo não são equivalentes:
- “Se Gabriela corre, então Gabriela fica cansado.”
- “Se Gabriela não corre, então Gabriela não fica cansado.”
Isso ocorre pois, de acordo com a primeira proposição, Gabriela pode ficar cansado mesmo sem correr, o que torna a segunda proposição logicamente diferente.
Para representar as equivalências lógicas, podemos utilizar o símbolo “≡”.
Equivalências Lógicas fundamentais
Algumas equivalências formam a base de toda a lógica proposicional. São elas:
1) Dupla negação: ¬(¬P) ≡ P
- Negar duas vezes uma proposição equivale a mantê-la na forma original.
- Por exemplo, a negação de “Vinícius não estuda” é “Vinícius estuda”.
2) Comutatividade:
- P ∧ Q ≡ Q ∧ P
- P ∨ Q ≡ Q ∨ P
- A ordem dos termos não altera o resultado em conjunções (E) ou disjunções (OU).
3) Associatividade:
- (P ∨ Q) ∨ R ≡ P ∨ (Q ∨ R)
- (P ∧ Q) ∧ R ≡ P ∧ (Q ∧ R)
- A forma de agrupar as proposições não muda o valor lógico.
4) Distributividade:
- P ∧ (Q ∨ R) ≡ (P ∧ Q) ∨ (P ∧ R)
- P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R)
- A aplicação da propriedade distributiva ajuda a simplificar expressões lógicas complexas.
Leis de De Morgan
As Leis de De Morgan permitem a negação de expressões compostas. Elas mostram como a negação afeta operadores lógicos compostos, encontrando suas equivalências.
Lei de De Morgan para o operador “E”
A negação de uma conjunção deve ser feita da seguinte maneira:
- trocando-se o operador “E” por “OU”; e
- negando todas as proposições individuais.
Portanto, matematicamente: ¬(P ∧ Q) = (¬P) ∨ (¬Q)
Por exemplo:
- Proposição: “Pedro estuda e Maria trabalha”.
- Negação: “Pedro não estuda ou Maria não trabalha”.
Ou seja: se a frase original exige que ambos sejam verdadeiros, a negação será satisfeita se pelo menos um for falso.
Caso uma das proposições simples já seja negativa, realizamos sua negação retirando o “não”, como no exemplo a seguir:
- Proposição: “Pedro não estuda e Maria trabalha”.
- Negação: “Pedro estuda ou Maria não trabalha”.
Lei de De Morgan para o operador “OU”
Do mesmo modo, a negação de uma disjunção deve ser feita da seguinte maneira:
- trocando-se o operador “OU” por “E”; e
- negando todas as proposições individuais.
Portanto, matematicamente: ¬(P ∨ Q) = (¬P) ∧ (¬Q)
Por exemplo:
- Proposição: “Pedro viaja ou Maria se exercita”.
- Negação: “Pedro não viaja e Maria não se exercita”.
Nesse caso, como o “OU” original aceita que apenas uma condição seja verdadeira, a negação só será verdadeira se ambas forem falsas.
Novamente, caso uma das proposições simples já seja negativa, realizamos sua negação retirando o “não”, como no exemplo a seguir:
- Proposição: “Pedro viaja ou Maria não se exercita”.
- Negação: “Pedro não viaja e Maria se exercita”.
Sintetizando, portanto, as duas leis de De Morgan analisadas, temos o seguinte:
| Operador original | Fórmula da negação | Exemplo | Negação correta |
| E (∧) | ¬(P ∧ Q) = ¬P ∨ ¬Q | Pedro estuda e Maria trabalha | Pedro não estuda ou Maria não trabalha |
| OU (∨) | ¬(P ∨ Q) = ¬P ∧ ¬Q | Pedro estuda ou Maria trabalha | Pedro não estuda e Maria não trabalha |
Essas leis também ajudam a entender negações de proposições condicionais e bicondicionais, como veremos a seguir.
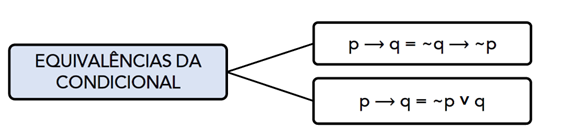
Equivalências Lógicas da Condicional (SE… ENTÃO)
A proposição condicional “Se P, então Q” pode aparecer em diversas formas equivalentes. As mais importantes são:
1) Forma original: P → Q
2) Forma equivalente: ¬P ∨ Q
- “Se P, então Q” é equivalente a “Não P ou Q”.
3) Contrapositiva (ou recíproca negada – volta negando): ¬Q → ¬P
- “Se Q é falso, então P é falso.”
Essas duas últimas são as equivalências lógicas fundamentais da condicional, frequentemente cobradas em concursos.
Por exemplo, considere a forma original: “Se estudo, então passo.”
- Equivalência 1: “Não estudo ou passo.”
- Equivalência 2 (contrapositiva): “Se não passo, então não estudei.”
Negação da Condicional
A negação de uma condicional não é outra condicional!
A regra prática é:
¬(P → Q) ≡ P ∧ ¬Q
Para ajudar na memorização, você pode utilizar a famosa regra da traição: “fica com a 1ª e nega a 2ª”. Por exemplo, a negação de “Se estudo, então passo” é “Estudo e não passo.”
Equivalências Lógicas da Bicondicional (SE E SOMENTE SE)
A bicondicional, representada por “↔”, é verdadeira quando as duas proposições têm o mesmo valor lógico (ambas verdadeiras ou ambas falsas).
Equivalências principais:
- P ↔ Q ≡ (P → Q) ∧ (Q → P)
- P ↔ Q ≡ (P ∧ Q) ∨ (¬P ∧ ¬Q)
- P ↔ Q ≡ ¬P ↔ ¬Q
Por exemplo, a proposição “Estudo se, e somente se, tenho tempo” é verdadeira quando estudo e tenho tempo, ou quando não estudo e não tenho tempo, sendo, portanto, equivalente a:
- “Se estudo, tenho tempo, e, se tenho tempo, estudo”; e
- “Estudo e tenho tempo ou não estudo e não tenho tempo.”
Como outro exemplo, considere a proposição “Corro se, e somente se, não estou cansado.” Essa proposição é logicamente equivalente a:
- “Não corro se, e somente se, estou cansado.”
Outras Equivalências Lógicas
Além das principais equivalências lógicas já vistas, apresentaremos duas equivalências menos cobradas, mas que podem fazer a diferença na hora da prova:
1) Bicondicional e disjunção exclusiva: ¬(P ↔ Q) ≡ P ⊕ Q
2) Negação da conjunção e condicional: ¬(P ∧ Q) ≡ P → ¬Q ≡ Q → ¬P
Resumo Comparativo – Equivalências Lógicas
Para te ajudar a revisar tudo o que vimos até aqui de forma estratégica, preparamos uma tabela com o resumo das principais equivalências lógicas:
| Tipo | Forma original | Forma equivalente | Observação prática |
| Condicional | P → Q | ¬P ∨ Q | “Se P, então Q” é igual a “Não P ou Q” |
| Contrapositiva | P → Q | ¬Q → ¬P | Troca a ordem e nega ambas |
| Negação da condicional | ¬(P → Q) | P ∧ ¬Q | Afirma P e nega Q |
| Bicondicional | P ↔ Q | (P → Q) ∧ (Q → P) | Duas condicionais simultâneas |
| Negação da conjunção | ¬(P ∧ Q) | (¬P) ∨ (¬Q) | Nega cada termo e troca o “E” por “OU” |
| Negação da disjunção | ¬(P ∨ Q) | (¬P) ∧ (¬Q) | Nega cada termo e troca o “OU” por “E” |
Finalizando – Equivalências Lógicas
As equivalências lógicas são ferramentas essenciais para interpretar, simplificar e transformar proposições em provas de Raciocínio Lógico. Compreender como aplicar as Leis de De Morgan, a contrapositiva da condicional e as relações entre bicondicional e disjunção exclusiva é decisivo para resolver questões rapidamente e sem erros. A chave para o domínio está na prática.
É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. Além disso, é fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança.
Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de equivalências lógicas que aparecer na sua prova.
Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível.
Bons estudos e até a próxima!
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!
Concursos Abertos
Concursos 2025
Fonte: Estratégia Concursos

