Fique por dentro – média, moda, mediana e quartis

Aprenda os conceitos essenciais sobre as principais medidas de posição com um resumo para as mais diversas provas de concursos.

Olá, pessoal! Tudo bem com vocês?

Quando se trata de Matemática, Estatística e Análise de Dados, alguns temas são recorrentes nos mais variados tipos de concurso. É o caso das medidas de posição, assunto presente em editais de bancas como FGV, CEBRASPE e FCC. Essas medidas ajudam a resumir e interpretar conjuntos de dados, oferecendo uma visão clara da tendência central e da distribuição.

Neste artigo, apresentaremos um resumo objetivo sobre as principais medidas de posição, para que você possa revisar a matéria de forma rápida e estratégica.

Confira os tópicos que serão abordados:

• O que são medidas de posição;
• Média;
• Moda;
• Mediana;
• Quartis;
• Tabela comparativa.

O que são medidas de posição

As medidas de posição indicam pontos de referência em um conjunto de dados numéricos. Elas servem para identificar onde se concentra a maior parte das observações ou como os valores se distribuem em relação a um ponto central.

Essas medidas são essenciais porque permitem transformar uma lista extensa de números em informações compreensíveis. Em provas de concursos, elas aparecem tanto em cálculos diretos quanto em questões interpretativas, muitas vezes apresentadas em tabelas e gráficos.

1) Média aritmética simples

A média aritmética simples é a medida de posição mais conhecida. Para calculá-la, basta somar todos os valores do conjunto e dividir pelo número de elementos. Nesse caso, consideramos que todos os valores possuem o mesmo peso dentro do conjunto.

Exemplo: Um aluno tirou as seguintes notas ao longo de um bimestre: 6, 7, 8, 9.

A média aritmética será:

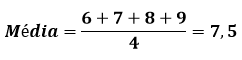
2) Média aritmética ponderada

Na média aritmética ponderada, cada valor do conjunto tem um peso diferente. Essa é a medida de posição que costuma ser utilizada para determinar a nota final de uma prova de concurso, por exemplo.

Dessa forma, devemos somar os produtos dos valores com seus respectivos pesos, e dividir o resultado pela soma dos pesos.

Exemplo: Um concurso é formado pelas disciplinas de português, matemática e estatística, tendo como pesos 1, 2 e 2, respectivamente. Assim, se um concurseiro tirar notas 8 em matemática, 6 em português e 4 em estatística, qual será a sua nota final?

A média aritmética ponderada será:

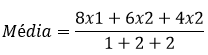
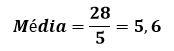
Moda

A moda é o valor que mais se repete em um conjunto de dados. Para encontrá-la, devemos calcular a frequência absoluta de cada valor dentro do conjunto. Além disso, é importante saber que o conjunto pode ser:

• Amodal: quando todos os valores aparecem apenas uma vez e, portanto, não há moda.
• Unimodal: um valor é o mais frequente.
• Bimodal: dois valores aparecem com a mesma frequência máxima.
• Multimodal: mais de dois valores aparecem com a mesma frequência máxima.

Exemplo: Seja um conjunto composto pelos valores 2, 4, 4, 5, 5, 7.

Nesse caso, o conjunto possui duas modas: 4 e 5, e, portanto, trata-se de um conjunto bimodal.

Mediana

A mediana é a medida de posição que representa o valor central do conjunto quando os dados estão ordenados em ordem crescente. Ou seja, devemos ordenar o conjunto de dados antes de encontrar a mediana. Nesse sentido, dividiremos os exercícios em dois casos:

a) Se o número de elementos for ímpar, a mediana é o valor que ocupa a posição central.

Exemplo: Conjunto formado por 8, 7, 12, 3, 15.

Ordenando os valores, temos: 3, 7, 8, 12, 15. Portanto, a mediana é o 8.

b) Se o número de elementos for par, a mediana é a média aritmética dos dois valores centrais.

Exemplo: Conjunto formado por 8, 6, 5, 10.

Ordenando os valores, temos: 5, 6, 8, 10. Dessa forma:

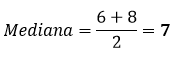
Quartis

Os quartis são uma medida de posição presentes em gráficos do tipo “box-plot” e dividem o conjunto de dados em quatro partes iguais, cada uma com 25% dos valores.

• Q1 (primeiro quartil): corresponde a 25% dos dados (mediana da metade inferior).
• Q2 (segundo quartil): corresponde à mediana (50%).
• Q3 (terceiro quartil): corresponde a 75% dos dados (mediana da metade superior).

Exemplo: Conjunto formado por 4, 6, 7, 8, 10, 12, 15, 18.

• Q1 = 6,5 (mediana da metade inferior – 4, 6, 7, 8).
• Q2 = 9 (mediana geral).
• Q3 = 13,5 (mediana da metade superior – 10, 12, 15, 18).

As questões de quartis são menos frequentes que média, moda e mediana, mas são recorrentes em concursos de áreas fiscais e bancárias, por exemplo.

Comparação entre as medidas de posição

Por fim, para te ajudar a revisar tudo o que vimos até aqui, preparamos uma tabela com um resumo das quatro medidas de posição presentes neste artigo:

Medida	Definição	Exemplo
Média	Soma dos valores : nº de elementos	Notas: 2, 5, 2 – Média = 3
Moda	Valor que mais se repete	Idades: 20, 22, 22, 25 – Moda = 22
Mediana	Valor central (dados ordenados)	Conjunto: 5, 7, 9 – Mediana = 7
Quartis	Dividem os dados em 4 partes (25%, 50%, 75%)	Conjunto: 1, 2, 3, 4 – Q1 = 1,5 / Q2 = 2,5 / Q3 = 3,5

Finalizando – medidas de posição

As medidas de posição — em especial média, moda, mediana e quartis — são fundamentais para a análise de dados e aparecem com frequência em provas de concursos. Cada medida fornece uma perspectiva diferente sobre o conjunto numérico, permitindo assim a identificação tanto da tendência central quanto da dispersão dos valores.

Ao estudar esse tema, lembre-se de que em provas de concursos, a habilidade de interpretar rapidamente os dados e aplicar a fórmula correta é tão importante quanto conhecer a teoria. A chave para o domínio está na prática.

É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. Além disso, é fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança.

Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de medidas de posição que aparecer na sua prova.

Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível.

Bons estudos e até a próxima!

Cursos e Assinaturas

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!

Concursos Abertos

Concursos 2025