Acesse o conteúdo completo – Sequências Numéricas
Aprenda os conceitos essenciais de Sequências Numéricas com um resumo para as principais provas de concursos.

Olá, pessoal! Tudo bem com vocês?
Quando se trata de Matemática e Raciocínio Lógico, alguns temas são recorrentes nos mais variados tipos de concurso. É o caso das famosas Sequências Numéricas, assunto presente em editais de bancas como FGV, CEBRASPE e FCC.
Neste artigo, apresentaremos um resumo objetivo dos principais conceitos e fórmulas sobre Sequências Numéricas, para que você possa revisar a matéria de forma rápida e estratégica.
Confira os tópicos que serão abordados:
- Conceitos gerais;
- Classificação das sequências numéricas;
- Lei de formação das sequências numéricas;
- Progressão aritmética;
- Progressão geométrica;
- Comparação entre progressão aritmética e geométrica;
- Dicas práticas para a prova.
Conceitos gerais de sequências numéricas
Uma sequência numérica é uma lista ordenada de números dispostos de acordo com uma determinada regra ou ordem lógica. Cada número que compõe a sequência é chamado de termo. É importante ressaltar que o posicionamento importa: mesmo que os números sejam os mesmos, alterar a ordem gera uma sequência distinta.
Os termos são, geralmente, descritos com a letra a, seguida do índice de sua posição.
a1 é o primeiro termo da sequência, a2 é o segundo termo, a3 é o terceiro termo, e assim por diante. As posições são ordenadas da esquerda para a direita, e os termos costumam ser colocados entre parênteses. Assim, a sequência fica:
(a1, a2,a3,…)
Exemplos:
- Sequência A: (1, 3, 5, 7, 9)
- Sequência B: (9, 7, 5, 3, 1)
Classificação das sequências numéricas
Existem duas principais maneiras de classificar uma sequência numérica, como veremos a seguir:
1) Classificação quanto à quantidade de termos
a) Sequência numérica finita
Uma sequência é finita se ela possui uma quantidade limitada de termos.
Exemplo: (2, 4, 6, 8, 10)
b) Sequência numérica infinita
Uma sequência é infinita se ela possui uma quantidade ilimitada de termos.
Exemplo: (10, 100, 1.000, 10.000,…)
2) Classificação quanto ao comportamento
a) Sequência numérica crescente
Uma sequência é crescente quando qualquer termo é sempre menor do que os seus sucessores.
Exemplo: (-2, -1, 0, 1, 2)
b) Sequência numérica decrescente
Uma sequência é decrescente quando qualquer termo é sempre maior do que os seus sucessores.
Exemplo: (10, 6, 2, -2, -6,…)
c) Sequência numérica constante
Uma sequência é constante quando todos os termos são iguais.
Exemplo: (1, 1, 1, 1, 1, 1)
d) Sequência numérica oscilante
Uma sequência é oscilante quando há termos alternados, ou seja, maiores e também menores do que os seus antecessores.
Exemplo: (1, -2, 4, -8, 16, -32,…)
Lei de formação das sequências numéricas
A lei de formação é a regra que determina como cada termo da sequência é obtido a partir de outros termos ou de sua posição. É a fórmula que gera os termos da sequência numérica. Contudo, as provas não costumam trazer a regra pronta – é preciso identificá-la analisando o padrão.
É importante entender que toda sequência possui uma lei de formação, que determina o valor de cada termo. Essa lei pode ser explícita (fórmula direta) ou recorrente (baseada no termo anterior). Nos concursos, identificar rapidamente essa lei é o primeiro passo para resolver questões de sequências numéricas.
Exemplo:
A lei de formação dos números ímpares (1, 3, 5, 7,…) é an = 2n – 1, onde n é o número do termo. Dessa forma:
a1 = 2.1 – 1 = 1
a2 = 2.2 – 1 = 3
a3 = 2.3 – 1 = 5
Exemplo 2:
A lei de formação an = 2.an-1 permite o cálculo de qualquer termo da sequência a partir de seu antecessor. Se o primeiro termo da sequência for 1, teremos:
a1 = 1
a2 = 2.1 = 2
a3 = 2.2 = 4
E, portanto, a sequência é (1, 2, 4,…).
Progressão aritmética (PA)
As progressões aritméticas são sequências numéricas especiais em que cada termo, a partir do segundo, é obtido somando o termo anterior a uma constante, chamada razão (r).
Dessa forma, a fórmula do termo geral (lei de formação) é dada por:
an = a1 + (n-1).r
Onde:
a1: primeiro termo
r: razão (diferença entre dois termos consecutivos)
n: posição do termo desejado na sequência
A soma dos n primeiros termos da PA é dada por:
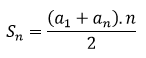
Exemplo:
Em uma PA de 10 termos, sendo a1 = 5 e a10 = 32, determine a soma de todos os termos.
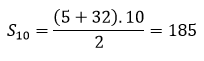
Progressão geométrica (PG)
As progressões aritméticas são sequências numéricas especiais em que cada termo, a partir do segundo, é obtido multiplicando o termo anterior por uma constante chamada razão (q). Problemas de juros compostos e crescimento populacional utilizam frequentemente questões de PGs nos concursos.
Desse modo, a fórmula do termo geral (lei de formação) é dada por:
an = a1.qn-1
Onde:
a1: primeiro termo
q: razão (divisão entre dois termos consecutivos)
n: posição do termo desejado na sequência
Exemplo:
Determine o 5º termo de uma PG que possui a1 = 2 e q = 3.
a5 = 2.34 = 162
Para uma PG finita, a soma dos n primeiros termos é dada por:
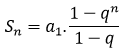
Já para uma PG infinita, com razão 0 < q < 1, a soma de todos os termos é dada por:
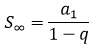
Comparação entre progressão aritmética e geométrica
Para não errar na prova, é fundamental compreender as principais características e diferenças entres as fórmulas de progressão aritmética e progressão geométrica.
| Conceito | Progressão Aritmética (PA) | Progressão Geométrica (PG) |
| Fórmula do termo geral | an = a1 + (n-1).r | an = a1.qn-1 |
| Característica | Diferença constante (r) | Razão constante (q) |
| Soma dos n primeiros termos | 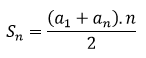 | 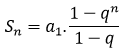 |
| Exemplo | (2, 4, 6, 8,10,…) | (1, 2, 4, 8, 16,…) |
Dicas práticas para a prova
Ao se deparar com uma questão de sequências numéricas, você pode seguir alguns passos para decidir qual fórmula utilizar:
- Verifique a diferença e a razão primeiro — ajuda a eliminar alternativas rapidamente.
- Procure padrões ocultos — quadrados perfeitos, cubos, números primos, fatoriais.
- Considere padrões alternados — muitas bancas usam duas ou mais sequências intercaladas.
- Use termos iniciais para achar a fórmula — teste n = 1, 2, 3 e veja se bate.
- Cuidado com pegadinhas — sequências podem mudar a regra no meio.
- Faça contas limpas e rápidas — rascunho organizado é um diferencial.
- Treine com questões de diferentes bancas — FGV e CESPE, por exemplo, têm estilos bem distintos.
Finalizando – sequências numéricas
Sequências numéricas é um tema essencial para quem deseja alcançar um bom desempenho em concursos públicos. Dominar conceitos como lei de formação, progressão aritmética e progressão geométrica aumenta significativamente as chances de acerto em questões de Matemática e Raciocínio Lógico.
A chave para esse domínio está na prática: resolva exercícios variados, preste atenção às diferenças e razões entre os termos, e treine o reconhecimento de padrões menos óbvios. Além disso, lembre-se de que as questões muitas vezes exploram pegadinhas, números negativos, frações ou até a combinação de diferentes tipos de sequências de números em um mesmo enunciado.
É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. É fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança.
Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de Sequências Numéricas que aparecer na sua prova.
Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível.
Bons estudos e até a próxima!
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!
Concursos Abertos
Concursos 2025
Fonte: Estratégia Concursos

